红黑树

红黑树的性质

1. 红黑树的根节点都是黑色的

2. 不能重现连续的红色(红色节点的子节点必须是黑色)

3. 所有叶子节点（NIL / null）被视为黑色

4. 从任一节点到其所有后代叶子节点的路径上，包含相同数目的黑色节点

5. 节点要么是红色要么是黑色

记法：左根右(二叉搜索树)，根叶黑，不红红，黑路同

插入规则

插入节点和正常的二叉树一样插入(默认插入的是红色的节点，红色比黑色更不容易破坏平衡)，插入之后可能破坏了平衡，所以需要从下到上调整。

可能出现三种情况

parent = cur.parent，grand = parent.parent，uncle = grand

插入节点是根节点

直接染成黑色

插入节点的叔叔是红色

parent和uncle设为黑，grand设为红色，将cur指向grand,继续向上修复

插入节点的叔叔是黑色

LL：

parent和cur都是左节点

LR：

parent和cur一左一右

RR：

parent和cur都是右节点

RL：

parent和cur一右一左

LL

grand右旋，对旋转点(grand)和中心点(parent)进行变色

旋转前

      G(B?)
     /
   P(R)
  /
 z(R)

旋转+变色

     P(B)
    /   \
  z(R)  G(R)

LR

parent左旋，grand右旋。对旋转点(grand)和中心点(z)进行变色

旋转前

    G
   /
  P
   \
    z

旋转+变色

     z(B)
    /   \
  P(R)  G(R)

RR

grand左旋，对旋转点(grand)和中心点(parent)进行变色

旋转前

 G
  \
  P(R)
   \
   z(R)

旋转+变色

   P(B)
  /   \
 G(R) z(R)

RL

parent右旋，grand左旋。对旋转点(grand)和中心点(z)进行变色

旋转前

  G
   \
    P
   /
  z

旋转+染色

     z(B)
    /   \
  G(R)  P(R)

总结：LL和RR都是G向反方向(R/L)旋转，LR和RL都是P先L/R旋转，G再R/L旋转

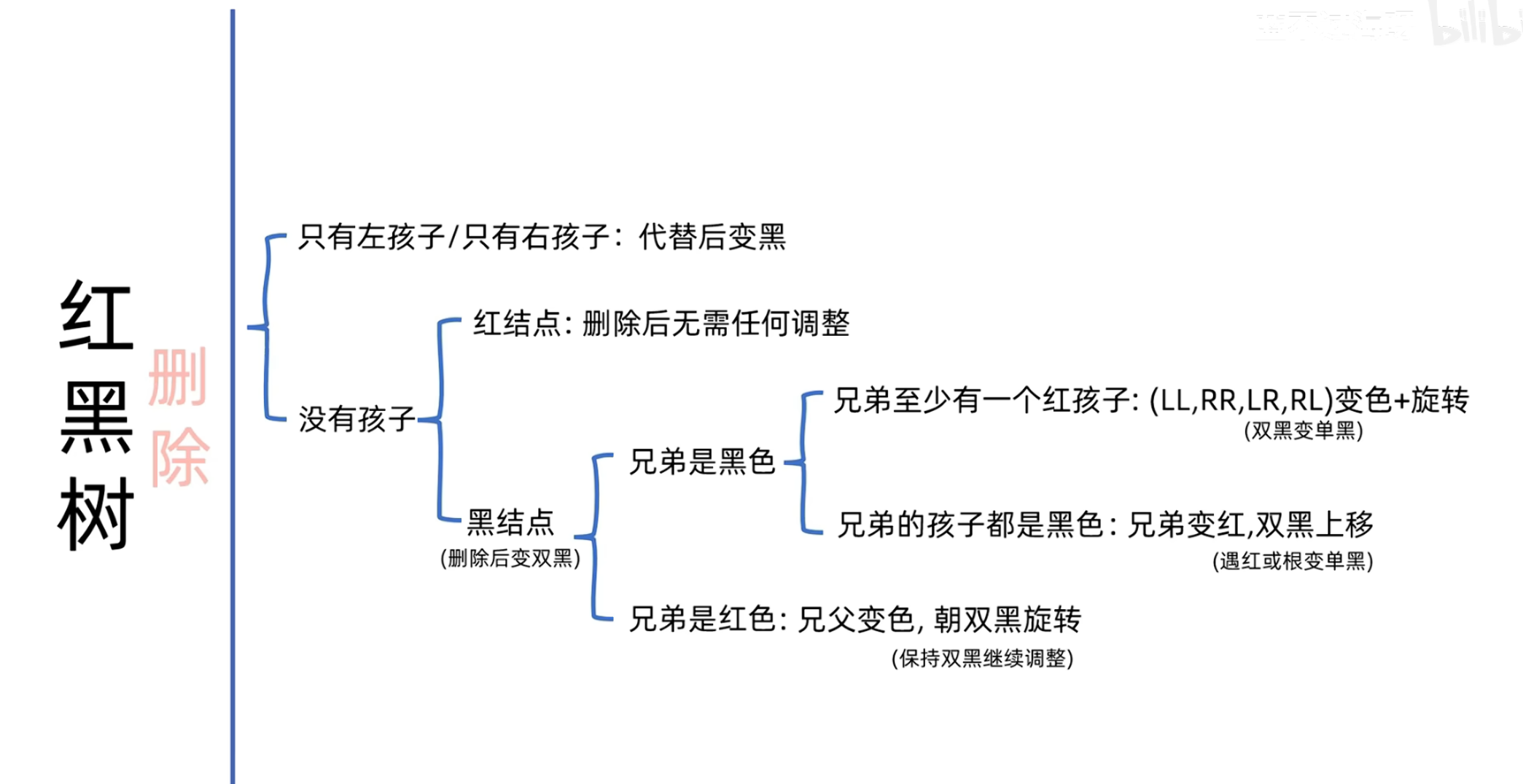
删除规则

左右都有孩子

• 后继：“中序遍历中，紧跟在当前节点之后的那个节点”，即 比 x 大的最小值。

• 前驱：“中序遍历中，紧挨在当前节点之前的那个节点”，即 比 x 小的最大值。

规则：先找到“中序后继”或“中序前驱”来替换它的值，然后再删除那个后继/前驱节点。一般默认为后继

没有孩子

红节点：直接删除即可

⭐黑节点：将null设置为双黑节点(这个节点是黑色，并算两个)

• 兄弟节点是黑色

  • 兄弟至少有一个红孩子:(LL,LR,RR,RL)变色+旋转

    • LL：兄弟在父节点左侧并且至少有左孩子是红色

      处理前

              P
             / \
         (B)S   D(BB)
           /
          R(R)

      R 变成 S 的颜色

      S 变P

      P 变黑

      对 P 执行 右旋

      双黑变单黑

      处理后：

             S(原P色)
            / \
         R(B)  P(B)
                 \
                 D(B)

    • RR：兄弟在父节点右侧并且至少有右孩子是红色

      处理前

          P
         / \
      D(BB)  S(B)
               \
                R(R)
      

      R 变成 S 的颜色

      S 变P

      P 变黑

      对 P 执行 左旋

      双黑变单黑

      处理后

              S(原P色)
             / \
          P(B)  R(B)
         /
       D(B)

    • LR：兄弟节点在左侧并且至少有右孩子是红色

      处理前

              P
             / \
          (B)S   D(BB)
             \
              R(R)

      R 变成 P 原来的颜色
      P 变黑
      对 S 左旋，再对 P 右旋
      双黑变单黑
      处理后：

              R(原P色)
             / \
          S(B)  P(B)
                  \
                  D(B)

    • RL：兄弟节点在右侧并且至少有左孩子是红色

      处理前

              P
             / \
          D(BB)  S(B)
                 /
               R(R)

      R 变成 P 原来的颜色

      P 变黑

      对 S 右旋，再对 P 左旋

      双黑变单黑

      处理后

              R(原P色)
             / \
          P(B)  S(B)
         /
       D(B)

  • 兄弟的孩子都是黑色：兄弟变黑，双黑上移(遇红或根变单黑)

            P
           / \
        S(B)   D(BB)
       / \
     L(B) R(B)

    1. 将 S 染成 红色
    2. 将 D(BB) 的双黑“向上转移”：即把 P 作为新的双黑节点处理（D = P）

    如果 P 原来是红色，则：

    • 把 P 染黑（双黑消除，修复结束）

    如果 P 原来是黑色，则：

    • 把 P 当作新的 D(BB)，继续向上修复（递归或循环）

• 兄弟节点是红色：兄父变色，朝双黑旋转

      P
     / \
  D(BB)  S(R)
         / \
      L(B) R(B)
  

  交换颜色：P 染红，S 染黑

  如果兄弟在右，则对 P 左旋；兄弟在左，则对 P 右旋。

  旋转后，新的兄弟一定是黑色，问题转化为前面的“兄弟为黑色”情况，继续处理。

只有左孩子/只有右孩子

孩子代替，然后变黑即可

总结

图片